K. Marinas' Cyclic Multiverse Hypothesis

This article is a working preliminary draft, NOT yet submitted for peer review. Leave your comments on the discussion page (talk page) or contact the First Author, kmarinas86, at their talk page or by email.

I, K. Marinas, am the founder of my Cyclic Multiverse Hypothesis^[1], in which I propose that universe is a fractal, as an alternative to the Big Bang Theory. My idea is not science as of yet, since the vast majority of detailed cosmological data and computing power is outside of my reach. Another reason why it is not science right now is because it is not being studied by staff of a university. This page is not something you can nor should cite for a school project. Meanwhile, I think that my idea lacks the errors of previous alternatives to the Big Bang Theory.

This is not wikipedia.

Illustrations

Mainstream

Map of cosmic microwave background radiation which fills the entire sky. Created by WMAP.

This picture shows distant galaxies, very distant blue galaxies, and a portion of the map of the Cosmic Background Radiation.

Visual aids depicting a fractal universe

Visual aids for this Cyclic Multiverse Hypothesis

This is an image of the Cyclical Multiverse Hypothesis of May 2004.

This is an image of the Cyclical Multiverse Hypothesis of March 2006.

A graphic showing how much of the sky a few TeraQuasars would cover.

The zoom-out effect

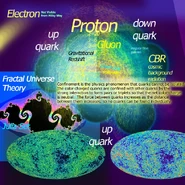
A Fractal Universe and Physical Units

The Cyclic Multiverse is a self-similiar fractal which might have formed just like a snowflake would. Anything from the curvature of movement to the pattern of a snowflake can ultimately explained with units of measurement.

$k$ is equal to the multiple between fractal levels.

Parent fractal's level

Our fractal's level

Depiction of the difference between different fractal levels (zooming in from left to right)

If our fractal's level is represented by the person on the right side of the above image, then our parent fractal's level is represented by the person on the left side of the above image. The primary physical properties for a particle or body (such as a proton, or turtle, etc.) existing in our fractal's level can be compared with similar-in-kind entity (e.g. a proton, or turtle, etc.) in the parent fractal's level. Properties of the parent fractal's level would differ from those of our fractal's level by scale factors derived from a length scale factor $k$ raised to various integer exponents as follow:^[2]

Scale factors

[k²] mass and time

$k^2$

Life, stars, and galaxies in the parent fractal's level are much larger than in our own.
The masses of a parent fractal's level are larger too.

mass	kg	kilograms
time	s	seconds

[k¹] wavelength, radius of gyration, (net) charge

$k^1$

Life, stars, and galaxies in the parent fractal's level are much larger than in our own.
Their wavelengths are larger.
The number of charged particles for a similar-in-kind object in our parent fractal's level is larger by a factor of $k^2$ compared to those of our fractal's level, but the net charge is less than $k^2$ as great due to cancellation of positive versus negative charge, for that is how net charge is determined. The cancellation reduces net charge by a factor of $k^{-1}$. The total factor increase of net charge going from our fractal's level to our parent fractal's level is therefore $k^{2-1}=k^{1}$.
The reason for this cancellation factor $k^{-1}$ is that, of the charges located within a given fractal's level, one kind of charge (negative) exceeds another kind of charge (positive) by an amount equal to their total quantity $k^2$ raised to an exponent of $\frac{1}{2}$, or in other words, the difference is the square root of their total quantity.
If quantity of charge is treated as an integer value, then this means that the quantity of negative charges is a triangular number by one index greater than the quantity of positive charge, also a triangular number.
If $k=10^{41}$, then the number of total charges of similar-in-kind object in our fractal's level compared to the child fractal's level is $k^2=10^{82}$. The index for the triangular number matching the negative charges is $k$, while the index for the triangular number matching the positive charges is $k - 1$.
So, for a similar-in-kind object in our parent fractal's level, the number of negative charges would be greater by a factor of $q_{-}=\frac{k*(k+1)}{2}$ while the number of positive charges would be greater by factor of $q_{+}=\frac{(k-1)*k}{2}$. The sum is $\frac{k\left((k+1)+(k-1)\right)}{2}=k^2=10^{82}$ while the difference is $\frac{k\left((k+1)-(k-1)\right)}{2}=k=10^{41}$. In this way, the net charge varies according to the square root of the total charge.
However, more importantly, with the indices of the triangular numbers for positive and negative charges being different by one, the number of parings between opposite charges $q_{-}*q_{+}$ is made equal to the number of parings between like charges $\frac{q_{-}*(q_{-}-1)}{2}+\frac{q_{+}*(q_{+}-1)}{2}$. In this way, the attractive and repulsive electrostatic forces, respectively, are balanced for a random charge distribution.

Provided the above is given, the converse is that particles of our fractal's level have $k^{1-2}=k^{-1}$ as much charge value as similar-in-kind objects in our parent fractal's level.

wavelength	m	Meters
radius of gyration	m/radian = r	a measure of the size of an object, a surface, or an ensemble of points. calculated as the root mean square distance of particles from the center of gravity or a given axis
charge	C	Coulombs

[k^-2] frequency, temperature, luminous intensity

$k^{-2}$

Life, stars, and galaxies in the parent fractal's level are much larger than in our own.
While mass of similar-in-kind objects of our parent fractal's level are larger by a factor of $k^2$ with respect to our fractal's level, the frequency, temperature, and luminous intensity of our parent fractal's level is less by a factor of $k^{-2}$.

frequency	1/s or radians/s	Hertz
temperature	K	Kelvin
luminous intensity	Cd	Candelas

[k⁰] scale-invariant properties

$k^{0}$

Some properties of similar-in-kind objects stay well within an order of magnitude between fractal's levels. These also include so-called "dimensionless" quantities.

Scale invariants

radians	[dimensionless] radians = arc length / radius	standard unit of angular measure
steradians	[dimensionless] steradians= surface / radius^2	standard unit of angular measure
moles	mol	standard unit of chemical measure
porosity	[dimensionless] m3/m3	measure of the void (i.e., "empty") spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%
constrictivity	[dimensionless] m/m	a function of the ratio of the diameter of the diffusing particle to the pore diameter
tortuosity	[dimensionless] m/m or m^2/m^2	[2D] ratio of the length of the curve (L) to the distance between the ends of it (C) [3D] Definitions include: arc-chord ratio arc-chord ratio divided by number of inflection points integral of square of curvature the Euclidean distance sums of the centroids of a pore divided by the length of the pore

From these assumptions, we can determine the difference of physical properties existing between successively greater parent fractal levels - to the infinitely larger. The properties can also be extended to child fractal levels - to the infinitely smaller.

The physical properties for our parent fractal's level compared to that of our level are as follows:

Quanta (q) [k¹=k^2-1]

$k^1$

Mechanical Phenomena

momentum	p=N·s=kg·m/s	coordinate force * time. mass * velocity.
wavelength	Meters	m
volume flow rate volumetric flux	m3/s	the volume of fluid that flows past a given cross sectional area per second

Electromagnetic Phenomena

electric charge	C=A·s	quantity of electric charge itself [Quantized]
magnetic flux	Wb=V·s	over time, voltage not dissipated through electrical current and resistance (I*R) and not stored in the form of electrical potential (Energy / Charge) manifests as magnetic flux (time integral of inductive voltage). (weber, Wb) [Quantized]

Quantum pair (q·q) [k²=k^2-1·k^2-1]

$k^2$

Gravitational Phenomena

mass

kg

inertial mass = gravitational mass

Mechanical Phenomena

angular momentum

L=J·s

quantity of action

Temperature Phenomena

heat capacity	J/K	proportion relating the amount of energy per Kelvin
entropy	J/K	thermodynamic disorder

Electromagnetic Phenomena

charge pair	C2	the primary component of electrical fields with existing, non-zero potential
magnetic helicity	Wb2	the extent to which a magnetic field "wraps around itself"
electrical capacitance	C/V=C2/J	charge stored per volt (farads)
magnetic inductance	Wb/A	magnetic flux stored per amp
magnetic permeance	Wb/A	magnetic flux stored per amp-(turn)2
planck's constant	J·s	the discrete quantity of action (quantum unit of angular momentum)

Inverse properties [k^-2]

$k^{-2}$

Electromagnetic Phenomena

elastance	V/C=J/C2	voltage demanded per charge (inverse capacitance)
reluctance	A2/J	current demanded per magnetic flux (inverse permeance)

Quantum flow or gyration (q/s) [k^-1=k¹/k²]

$k^{-1}$

Gravitational Phenomena

mass density

kg/m3

Mechanical Phenomena

force	p/s=N=J/m	momentum per second. comes from an energetic kinetic potential produced by an impulse.
velocity	m/s	meters per second.
dynamic viscosity	(kg/s)/m	the resistance of a fluid to deformation under shear stress
hydraulic conductivity	m/s	a property of vascular plants, soil or rock, that describes the ease with which a fluid (usually water) can move through pore spaces or fractures. it depends on the intrinsic permeability of the material and on the degree of saturation, and on the density and viscosity of the fluid.

Temperature Phenomena

thermal conductivity	(W/m)/K	ability of a material to conduct heat.
Wien's displacement constant	m·K	the relationship between peak wavelength and temperature of a blackbody radiation spectrum within a given fractal's level

Electromagnetic Phenomena

current	A=C/s	charge per second.
voltage	W/A=J/C=Wb/s	magnetic flux per second. energy per unit charge. power per unit current. (volt)
electrical conductivity	1/(Ω·m)	property of matter which allows an electric field to get from A to B
electric flux density (D-field) or electric displacement field electric polarization (P-field)	C/m2	units of current per circulation. units of charge per area. electric dipole moment per volume.
magnetic flux density (B-field) or magnetic induction	Wb/m2=T	units of voltage per circulation. units of magnetic flux per area. magnetic dipole moment (magnetic pole definition) per volume.
gyromagnetic ratio	C/kg	the ratio of a particle's magnetic dipole moment (current loop definition) to its angular momentum.

Light Phenomena

spectroscopic wavenumber

2 pi radians/m = 1/r

2 pi radians divided by wavelength

Inverse properties [k¹]

$k^1$

Mechanical Phenomena

radius

r

radius of a curve at any point on a path (turning radius or radius of curvature)

Temperature Phenomena

thermal resistivity	(K·m)/W	ability of a sample of material to resist the flow of heat
velocity change with temperature	(m/s)/K	the temperature change required to change the velocity by a certain amount is less for a similar-in-kind of object in our parent fractal's level, or conversely, the same temperature has greater effect on the velocity.

Electromagnetic Phenomena

electric resistivity	Ω·m	property of matter which resists an electric field from getting from A to B
electric permittivity	C/(V·m)	resists the flow of an electric field, contains charge
magnetic permeability	N/A2	in the positive sense, a measure of the ability of a material to support the formation of a magnetic field within itself. in the negative sense, the amount of resistance encountered when forming a magnetic field in a medium.
magnetic dipole moment (current loop definition)	A·m2	a vector whose direction is normal to a loop of current. proportional to current and area.

Light Phenomena

wavelength distance

m

influences electrical and acoustical properties

Coupling a quanta (q) with a quantum flow or gyration (q/s) [k⁰=k¹·k^-1]

$k^{0}$

Mechanical Phenomena

energy	L·radians/s=J=kg·m2/s2	quantity of energy itself
torque	L/s=kg·m2/(s2·radians)	energy applied per radian of rotation to a member to produce rotational motion force applied to a member, times the moment of the member, to produce rotational motion
torsion	N·m	force applied to a member, times the moment of the member, to produce rotational deformation (twist)
torsion coefficient torsion elastic modulus	N·m/radians	force applied per radian of twist to a member, times the moment of the member, to produce rotational deformation (twist)
mass flow rate	kg/s	the mass of fluid that flows past a given cross sectional area per second
areal velocity	m2/s	area swept by a path per unit time
circulation	m2/s	the line integral around a closed curve of the velocity field
diffusion coefficient	m2/s	a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species
hydraulic transmissivity	m2/s	directly proportional to horizontal hydraulic conductivity and thickness

Temperature Phenomena

thermal conductance	(J/s)/K	rate of heat flow per temperature increment
entropy flux	(J/K)/s	rate of entropy flow

Electromagnetic Phenomena

electric flux	N·m2/C	comes from an electric charge
electrical conductance	A/V	current produced / (energy / charged particle)
conductance quantum	2·e2/h	the quantized unit of electrical conductance
quantum of circulation	(1/2)·h/me	half the ratio of the Planck constant to the mass of the electron
magnetic vector potential	N/A=Wb/m	force per amp. magnetic flux per meter.
fine structure constant	N·m/(N·m) = (m/s)/(m/s) = m/m = N/N = q^2/q^2 = dimensionless	See Fine structure constant#Physical interpretations on Wikipedia.

Photometric Phenomena

luminous energy	lm·s	quantity of light. living things on our parent fractal's level see photons, the corresponding of which have $k^{0}$ as much energy.
luminous efficacy	lm/W	power as it appears to an observer versus the actual power
luminous exposure	lm·s	the accumulated physical quantity of visible light energy (weighted by the luminosity function) applied to a surface during a given exposure time.

Radiometric Phenomena

radiant energy

J

radiated energy

Inverse properties [k⁰]

$k^{0}$

Mechanical Phenomena

kinematic viscosity	m2/s	ratio of dynamic viscosity to mass density
fixed-end moment	N·m	reaction moments developed in a beam member under load, with both ends held in place

Temperature Phenomena

thermal resistance

K/W

index of a material's resistance to heat flow the reciprocal of conductance

Electromagnetic Phenomena

electrical resistance

W/A2

lower electrical resistance at the our parent fractal's level (ohms Ω)

Coupling two quantum flows or gyrations (q/s) and (q/s) [k^-2=k^-1·k^-1]

$k^{-2}$

Gravitational Phenomena

angular velocity

radians/s=(m/s)/r

inverse of the orbital period

Mechanical Phenomena

vorticity	radians/s	local spinning motion equal to the curl of the velocity field
power	W=J/s	rate of energy expenditure
mass flux	(kg/s)/m2	flow of mass through an area
specific acoustic impedance	(kg/m^3)·(m/s)	proportional to the mass density and the phase velocity (speed of sound).
surface tension surface stress	J/m2	the amount of tension that keeps a surface, especially of liquids together the amount of tension required to deform a surface
stiffness spring constant	N/m	force / distance

Temperature Phenomena

temperature	K	objects of our parent fractal's level are colder than those of our fractal's level
thermal heat transfer coefficient	(W/m2)/K	coefficient, thermal conductance change of power flux density per temperature increment
entropy flux density	(W/K)/m2	entropy flux per area

Electromagnetic Phenomena

angular frequency	radians/s=(m/s)/r	inverse of the oscillation period
charge volumetric density	C/m3	charge per volume
magnetic flux volumetric density	Wb/m3	magnetic flux per volume
magnetization	A·m2/m3	magnetic dipole moment (current loop definition) per volume.
electric field strength (E-field)	V/m=N/C	units of volts per meter. force / charge.
magnetic field strength (H-field) magnetic polarization (M-field)	A/m	units of amps per meter. an auxillary field which causes magnetic flux.

Photometric Phenomena

frequency	1/s	influences electrical and acoustical properties (Hz, cycles per second)
angular frequency	radians/s	frequency with which phase changes
luminous flux	lm=Cd·sr	Candelas times Steradians (lumens, lm)
luminous intensity	Cd	power emitted by a light source

Radiometric Phenomena

radiant exposure

J/m2

the amount of light allowed to fall on each area unit

Inverse properties [k²]

$k^2$

Gravitational Phenomena

mass

kg

inertial mass = gravitational mass

Mechanical Phenomena

area	m2	surfaces
time	s	period of oscillation, translations, rotations, and other motions in general
hydraulic resistance	m/(m/s)	The resistance to vertical flow of a soil layer with a saturated thickness and vertical hydraulic conductivity
Fluid permeability	m2 = (m/s)·((N/m2)·s)/((N/m2)/m)	part of the proportionality constant in Darcy's law which relates discharge (flow rate) and fluid physical properties (e.g. viscosity), to a pressure gradient applied to the porous media

Temperature Phenomena

thermal expansion coefficient and temperature of color	1/K	the fractional change in length or volume per Kelvin at constant pressure
thermal resistance coefficient	K/(W/m2)	coefficient, thermal resistance

Electromagnetic Phenomena

electric dipole moment	C·m	a vector due to uneven distribution of unlike charges. proportional to charge and distance.
magnetic dipole moment (magnetic pole definition)	Wb·m	proportional to magnetic flux and distance.
electron electric dipole moment	e·centimeter	intrinsic property of an electron such that the potential energy is linearly related to the strength of the electric field

Chemical Phenomena

bond dipole moment	statcoulomb·centimeter	a measure of the polarity of a chemical bond within a molecule
molecular dipole moment	statcoulomb·centimeter	a measure of the polarity of a molecule

Radiometric Phenomena

etendue

m2·sr

a property of light in an optical system, which characterizes how "spread out" the light is in area and angle

Ether density [k^-3]

$k^{-3}$

Gravitational Phenomena

force/mass	m/s2
G	m3/(kg·s2)
pressure	N/m2

Mechanical Phenomena

energy density	J/m3	energy / volume
elastic modulus	N/m2	stress / strain
yield stress	N/m2	force / area sufficient to result in plastic deformation (time-asymmetric).
tensile stress	N/m2	force / area whose normal is parallel to force vector
Young's modulus	N/m2	tensile stress / tensile strain = tensile stress / ( change of length / initial length )
shear stress	N/m2	force / area whose normal is perpendicular to force vector
shear modulus	N/m2	shear stress / shear strain = shear stress / ( transverse displacement / initial length )
momentum flux	N/m2	the rate of transfer of momentum across a unit area

Electromagnetic Phenomena

current density

A/m2

current / area

Photometric Phenomena

luminous energy density

lm·s/m3

luminous energy density

Radiometric Phenomena

radiant energy density	J/m3	radiant energy density
spectral power	W/m	radiant power per wavelength
spectral intensity	W/(sr·m)	radiant intensity per wavelength

Inverse properties [k³]

$k^3$

Mechanical Phenomena

volume	m3	the amount of space
section modulus	m3	equal to the second moment of area (or moment of inertia) divided by the distance from the neutral axis to any given fibre

Quantum Oscillation Flux density ((qq/s²)/m²) [k^-4=k¹·k¹/k⁴/k²]

$k^{-4}$

Mechanical Phenomena

angular acceleration	radians/s2	rate of change of angular velocity (Hertz per second)
power flux	W/m2	rate of energy transfer through a given surface
particle flux	[number of particles]/(m2·s)	the rate of transfer of particles through a unit area
force density	N/m3	the negative gradient of pressure the flux density of the hydrostatic force

Temperature Phenomena

thermal flux	W/m2	rate of heat energy transfer through a given surface
heating rate cooling rate	K/s	rate of temperature change

Chemical Phenomena

diffusion flux

mol/(m2·s)

the rate of movement of molecules across a unit area

Photometric Phenomena

luminance	Cd/m2	light emission through a surface, per area
illuminance	lm/m2	light incident onto a surface, per area
luminous emittance	lm/m2	light emission from a surface, per area

Radiometric Phenomena

radiative flux radiative flux density	W/m2	power through a surface, per area.
irradiance radiant flux density	W/m2	power incident onto a surface, per area.
radiant excitance	W/m2	power emitted from a surface, per area
radiosity	W/m2	emitted plus reflected power leaving a surface, per area
radiance	W/(sr·m2)	power per unit solid angle per unit projected source area

Inverse properties [k⁴]

$k^4$

Mechanical Phenomena

moment of inertia	kg·m2	geometrical property of an area which reflects how its points are distributed with regards to an arbitrary axis
second moment of area moment of inertia of plane area area moment of inertia second area moment	m4 or m2r2 or r4	geometrical property of an area which reflects how its points are distributed with regards to an arbitrary axis
torsion constant	m4	geometrical property of a bar's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar

Temperature Phenomena

Stefan–Boltzmann constant

(W/m2)/K4

in a given fractal level, the total energy radiated per unit surface area of a black body in unit time (power flux density) is proportional to the fourth power of the temperature

Electromagnetic Phenomena

electric polarizability

C·m/(V/m)=C2·s2/kg

the ratio of the induced electric dipole moment to the electric field that produces this dipole moment

What this hypothesis requires

Cyclic Multiverse Hypothesis explains the redshifts of galaxies varying in distance by proposing two things:

1. TeraQuasars
2. Hyperbolic curvature of light paths

---

TeraQuasars

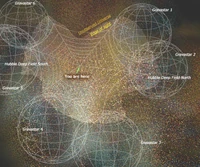
New kinds of collapsed masses called TeraQuasars. These are proposed celestial objects with the proposed mass of trillions of quasars located behind the furthest galaxies and stars we can see in the universe - see Hubble Deep Field.

1. Gravitational redshift is the decrease of a photon's frequency with increasing gravitational potential. This kind of redshift is directly linked with the curvature of the gravitational field.
2. Angular diameter distance of distant galaxies can be explained as being an effect caused by an immensely dense gravitational field situated in the background.

Concordance with WMAP

To explain the Cosmic Background Radiation, the Cyclic Multiverse Hypothesis requires that TeraQuasars are surrounded by an environment which has a similar (if not exactly the same) composition as the one described in the Big Bang theory of the "early" universe. This is analogous to quasars in the centers of galaxies which have a radiation intense environment surrounding them. This environment would be a shell surface that today's cosmologists call the surface of last scattering. However, in contrast to the idea of today's cosmologists - that the surface of the last scattering is a spherical shell concentric to the point of observation - in this Cyclic Multiverse Hypothesis, the surface of the last scattering occurs at ellipsoid-like surfaces of several TeraQuasars - at the same temperature (~3000K) and redshift (~1100).

Contrast from Black Holes

TeraQuasars cannot be thought of as black holes with the mass of trillions of galaxies. That is, because it is required by the Cyclical Multiverse Hypothesis that the TeraQuasars are surrounded by low entropy. This is the same kind of low entropy required by the early universe of the Big Bang Theory. A possible candidate is the Gravastar, which is described as having a very low entropy, in contrast to the high (even maximum) entropy of black holes. Also, with the Gravastar, matter has the ability to bounce back away, a theoretical feature which is necessary in this Cyclic Multiverse Hypothesis. Experiments will be needed to test theories involving Gravastar-like objects. The discovery of such an object would be consistent with this Cyclic Multiverse Hypothesis.

Contrast from Cyclic Big Bang/Big Crunch

Instead of an inflating singularity that collapses upon itself and reinflates etc., the Cyclical Multiverse Hypothesis proposes that the TeraQuasars are the source of new matter (predominately hydrogen) and that old and new matter can enter and exit the multimillion-light-year thick atmosphere of TeraQuasars. A fractal with a pattern that repeats towards the infinitely large scales and towards the infinitely small scales is necessarily heterogeneous in space at all levels, whereas many cyclic universe models based on the Big Bang Theory suggest that the universe is homogeneous and isotropic at large scales.

More on the size of TeraQuasars

Since TeraQuasars would be very large and exist behind a significant fraction of the sky, even more than the Andromeda Galaxy which itself spans 8 moon diameters, they would appear basically uniform and isotropic when viewed through the microwave spectrum. The TeraQuasars could also be accompanied by smaller partners, or GigaQuasars, which would be like TeraQuasars, but many times smaller.

---

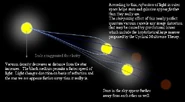
Hyperbolic curvature of light paths

The zoom-out effect caused by hyperbolic curvature of light paths

The zoom-out effect for stars

The zoom-out effect for galaxies

Hyperbolic curvature of light paths is an idea taken from Hyperbolic geometry applied to the motion of light.

1. Observations of galactic rotation velocities (see Galaxy rotation problem) and the brightness of distant supernovas (see Dark Energy) cause the author to suggest that the space outside our solarsystem, between the stars and between the galaxies is hyperbolic.
2. Consequences of Hyperbolic Geometry:
• Stars and galaxies would be dimmed by a factor different than the inverse-square law.
• The low-density space between the stars and between the galaxies would act like a concave (zoom out) lens. The parallaxes of stars would be smaller than it would be without the Hyperbolic curvature of space-time, which means that stars and galaxies would be closer than what would be believed if the space between stars was Euclidean. The galaxy would be smaller in diameter than it appears, however, the star count would remain valid.
• Having negative curvature between galaxies in clusters would make them appear farther apart than they really are. The required dark matter abundance would be reduced significantly.
• The observable part of our universe would be smaller than it appears, yet remains stable due to local gravitational repulsion within the gravity of the whole.

Determinant of the hyperbolic curvature of light paths

Observational constraint

Any proposed zoom-out effect must be able to account for any astronomical observations in order to be valid. One particular observation is the angular speed $\omega$ of Triangulum Galaxy (also known as Messier Object 33 (or M33)), which has been measured astrometrically using a wide-spread array of radio telescopes called the Very Long Baseline Array[3].

The radius $R$ of the galaxy M33 was inferred from the standard premises, after two things: 1) observing a Doppler redshift which give us velocity $V$, and 2) observing directly the angular speed of the galaxy using an array of radio telescopes separated by many thousands of kilometers. The radius of the galaxy $R$ may be determined by dividing the velocity $V$ by the angular speed $\omega$.

The introduction of distance variable $r$ results from a conjecture that radii of individual galaxies are less than they appear to be. The factor by which $R$ is greater than $r$ may be defined as the variable $e$ which stands for the exaggeration of distance caused by the zoom out effect. Since the value of angular speed $\omega$ does not disagree at all with the normal expectations of scientists, the variable $e$ must also imply the factor by which the velocity is exaggerated. Of course, the measured orbital velocity $V$ of masers in M33 is determined via the Doppler redshift equation, of which drastic modification ought to be avoided. Therefore, the new requirement is to divide $e$ from the $V$ deduced from the Doppler formula to get $v$ - the actual orbital velocity.

---

For quantification, a potential field must be defined.

Potential field

While elliptic curvature of light paths can be explained using the gravitational potential, the need for a hyperbolic curvature of light paths requires another potential having an opposite sign. Therefore, a new definition of potential energy at the cosmic level will be used by the Cyclic Multiverse concept that implements the effect of a hypothetical Hubble Vacuum Potential Energy (HVPE) that is rooted in the expansion that has been associated with Hubble's law.

$HVPE=\frac{1}{2}m(Hr)^2$

Where:

$r$ is equal to apparent distance between masses $M$ and $m$.

$H$ is the Hubble constant, which when multiplied by apparent distance $r$ gives us the hubble velocity.

$Hr$ is the Hubble velocity.

GPE is simply Gravitational Potential Energy which was discovered by Issac Newton.

$GPE=\frac{-GMm}{r}$

$U_{Galaxy}$ determines the field potential energy with respect to galaxies.

$U_{Galaxy}=GPE_{Galaxy}+HVPE_{Galaxy}=\frac{-GM_{Galaxy}m}{r_{Galaxy}}+\frac{1}{2}m(Hr_{Galaxy})^2$

Where:

$m$ is the mass subject to this potential.

$U_{TeraQuasar}$ determines the field potential energy with respect to a TeraQuasar. The sign of the potential is opposite of that for galaxies. Instead of an inverse square attractive force and a square repulsive potential, TeraQuasars have an inverse square repulsive force and a square attractive potential.

$U_{TeraQuasar}=-HVPE_{TeraQuasar}-GPE_{TeraQuasar}=\frac{GM_{TeraQuasar}m}{r_{TeraQuasar}}-\frac{1}{2}m(Hr_{TeraQuasar})^2$

Again, where $m$ is the mass subject to this potential.

The goal is to make the gravitational laws of the very large and very small alike:

• It is intended by K. Marinas that $U_{TeraQuasar}$ corresponds to a hypothesis in Quantum Chromodynamics (QCD) which involves a quadratic potential[4][5].
• Mario Everaldo de Souza[6] has hypothesized a hidden SU(2) substructure of quarks. He calls the new particles primons (a quark, he says, is composed of two of these). K. Marinas currently assumes this be the case, saying that one TeraQuasar corresponds to one of the primons in a single quark.

Quantitative Examples

In general, $U=-L\omega$ where:

$L$, the angular momentum, is equal to $\pm \; mvrsin(\pi/2)$ or simply $\pm \; mvr$.

$\omega$, the angular speed, which is the same as $\frac{v}{r}$.

Given $U_{Galaxy}$, the following are the initial steps for solving for exaggeration $e$:

$-L\omega=\frac{-GMm}{r}+\frac{1}{2}m(Hr)^2$

$0=\frac{-GMm}{r}+\frac{1}{2}m(Hr)^2+L\omega$

$0=\frac{-GMm}{r}+\frac{1}{2}m(Hr)^2+mv^2$

$0=\frac{-GMme}{R}+\frac{1}{2e^2}m(HR)^2+\frac{mV^2}{e^2}$

$0=\frac{-GMe}{R}+\frac{1}{2e^2}(HR)^2+\frac{V^2}{e^2}$

$0=\frac{-GM}{R}e^3+\frac{1}{2}(HR)^2+V^2$

By solving for $e$ in this cubic equation, the following solutions for $e$ can be found:

Situation	$M$	$R$	$V^2$	$e=\frac{R}{r}=\frac{V}{v}$
The Sun's orbit around the Milkyway	$9.5*10^{40}\ kg$	$26\ KLY$	$(220000\ m/s)^2$	$1.23$
Virgo cluster (visible mass only)	$4.5*10^{44}\ kg$	$20\ MLY$	$(1500000\ m/s)^2$	$2.46$
NGC 3877	$7.3*10^{40}\ kg$	$3.51*10^{20}\ m$	$(160000)^2\ m/s$	$1.23$
NGC 2903	$1.5*10^{41}\ kg$	$6.75*10^{20}\ m$	$(180000)^2\ m/s$	$1.30$
NGC 801	$3.5*10^{41}\ kg$	$1.62*10^{21}\ m$	$(210000)^2\ m/s$	$1.45$
NGC 4088	$8.2*10^{40}\ kg$	$6.75*10^{20}\ m$	$(168000)^2\ m/s$	$1.52$
NGC 6946	$7.4*10^{40}\ kg$	$8.1*10^{20}\ m$	$(160000)^2\ m/s$	$1.61$
NGC 6614	$1.7*10^{41}\ kg$	$1.75*10^{21}\ m$	$(182000)^2\ m/s$	$1.72$
NGC 3198	$4.8*10^{40}\ kg$	$8.1*10^{20}\ m$	$(155000)^2\ m/s$	$1.82$
UGC 6818	$2.5*10^{39}\ kg$	$2.16*10^{20}\ m$	$(73000)^2\ m/s$	$1.90$
NGC 3789	$2.2*10^{40}\ kg$	$1.08*10^{21}\ m$	$(114000)^2\ m/s$	$2.12$
UGC 6446	$4.6*10^{39}\ kg$	$4.59*10^{20}\ m$	$(83000)^2\ m/s$	$2.18$
NGC 1560	$1.8*10^{39}\ kg$	$2.43*10^{20}\ m$	$(77000)^2\ m/s$	$2.29$
UGC 7089	$2.5*10^{39}\ kg$	$3.51*10^{20}\ m$	$(82000)^2\ m/s$	$2.42$

Phenomenological extension

$U_{Galaxy}=0$ is the unstable equilibrium in which a galaxy may attract another if it were closer or repel if it was further.

$U_{TeraQuasar}=0$ is the stable equilibrium consistent with the surface of the last scattering, or the shell of the surface of a TeraQuasar.

$U_{Galaxy}$ goes from attraction to repulsion (negative to positive $U_{Galaxy}$) as distance increases.

$U_{TeraQuasar}$ goes from repulsion to attraction (positive to negative $U_{TeraQuasar}$) as distance increases.

Quark confinement of the higher fractal level

In this case, a TeraQuasar's maximum distance is approached and confinement approaches the point where taking the TeraQuasar any further, via an addition of background radiation (such as a high energy gamma ray from the parent fractal level), would result in one or more new TeraQuasars. Applies for: $U_{TeraQuasar}\approx \;-mc^2$ at largest radii with respect to TeraQuasars.

Quark production of the higher fractal level

In this case, galaxies travel at relativistic speeds with respect to the background radiation emitted by TeraQuasars, and because of this they become massive enough to become seeds which may or may not develop into the next TeraQuasar. Applies for: $U_{Galaxy}\approx \;mc^2$ at largest radii with respect to galaxies.

Super Quasar Production of our fractal level

In this case, a whole cluster of galaxies would be able to become a "super" quasar simply due to the attraction between them (i.e. without a "Tera"Quasar's influence). Formation of a quasar in this way may be more likely in TeraQuasar systems external to ours which are devoid of life. Applies for: $U_{Galaxy}\approx \;-mc^2$ at smallest radii with respect to galaxies.

Quantum Gravity of the parent fractal level

In this case, a TeraQuasar system (a system of Quarks of our parent fractal level) has a jumpy reaction following a collision with a particle (massive or non massive) from our parent fractal level (perhaps one inside in depths of a "super" quasar of our parent fractal level), which would result in a reflection off the upper boundary of "Q"uark confinement, $U_{TeraQuasar}\approx \;-mc^2$, at large radii. This may be the cause of a subsequent reflection off of the lower boundary, $U_{TeraQuasar}\approx \;mc^2$ (beneath the surface TeraQuasars themselves). During the subsequent reflection, the components of a TeraQuasar system of our fractal level overcome much of the repulsion that occurs amongst them. This would even require that the surfaces of these components (TeraQuasars) pass through one another. Merged TeraQuasars of our fractal level may be the compositional basis of second and third generation Quarks of our parent fractal level which are subject to decay. In order for a singularity be simulated, TeraQuasars of an infinitely small fractal level would have be to merged into third generation quarks within the third generation quark of a higher fractal level, repeated infinitely... followed by third generation quarks which are the composition of a TeraQuasar of our fractal level (equivalent to 1/2 a Quark of our parent fractal level). The impossibility of merging all constituent third generation quarks into a single point would prevent a singularity. Decay of some of these infinitesimal particles is more likely than merging the infinite number of these infinitesimal particles which make up a third generation quark inside the TeraQuasar into a single point. It would then follow that weak interaction proliferating inside particles of an infinity of fractal levels prevents the singularity. Applies for: $U_{TeraQuasar}\approx \;mc^2$ at the smallest radii with respect to TeraQuasars.

Rejected formulas

This approach has been favored against the following approaches for having non-problematic values of $e$ (1), for having relevance to Hubble observations (2), for sticking to correct concepts of Kinetic Energy (3), and for always having solutions (4).

For all the following formulas, $V$ is orbital velocity, which in these cases are approximately equal to $\sqrt{\frac{GM}{r}}$

 (1): $-U_{general}=mV^2e^2$
 (2): $U_{pioneer}=\frac{-GMm}{r}+mpr$, where $p$ is the anomalous pioneer acceleration.
 (3): $U_{hubble}=\frac{-GMm}{r}+m(Hd)^2$
 (4): $-U_{general}=mV^2$

Gravitational, Weak, Electromagnetic, and Strong forces

In the Cyclical Multiverse Hypothesis, the gravitational attraction of our fractal level becomes a binding force in the higher fractal level that:

1. opposes a nucleus' tendency to split apart (The Strong Nuclear Force)
2. becomes the attractive force between protons and electrons (The Attractive Electromagentic Force)

Similiarly, the gravitational repulsion defined by the mechanism above becomes a seperating force in the higher fractal level that:

1. decays massive particles (such as neutrons) into smaller ones (The Weak Force)
2. leads to CP-violation in antimatter (The Weak Force)
3. keeps the nucleus from becoming a black hole (The Repulsive Electromagentic Force)
4. prevents the electron from merging with a proton (depsite their opposite charge)
5. puts a limit on the number of electrons an element can have

If the universe were eternal, the weak force would have enough time to accumulate the observed difference between the amount of matter and antimatter. The remaining antimatter would be maintained by natural particle accelerators found inside extreme environments such as the center of the Milky Way.

These become the two fundamental forces (i.e. the binding force and the seperating force) of the universe. Both must exist in order for the fractal universe to be eternal and moderate.

Symmetry inside the fractal

Energy containment within a fractal level

According to the section #A Fractal Universe and Physical Units, similar-in-kind objects in different fractal levels have the same order of magnitude in energy.

Paradox This implies that if an exponential rate of decay, in the form of matter being converted into propagating electromagnetic waves, whose time parameter (or half-life) corresponded to the unit of time for the fractal level of said matter, then this would cause an outflow of energy which would make the relationship between energy and scale factor $k^n$ increasingly divergent, causing energy to concentrate to a fractal level in the infinitely large. Extrapolating the conditions of exponential decay to the infinitely small would cause our fractal level to have a very short life indeed, especially considering the very short duration of each of their cycles (gyration periods).

Resolution The resolution to this problem is that energy in a fractal level is contained within a fractal level in two ways:

1. By an upper boundary existing at the level of the immediate universe, somewhat larger than the volume currently visible to today's astronomers, which has dimensions of at least 10²⁶ meters.
2. By a lower boundary existing at the level of the positive nucleon (e.g. proton), which has dimensions of 10^-15 meters.

Possible effects of this resolution The energy associated with a fractal level can be seen as having a propagation velocity obeying a log-normal distribution. Wavelength, frequency, and energy within a fractal level may also obey a log-normal distribution within each fractal level. This has possible implications for any future statistical thermodynamic treatment of this model.

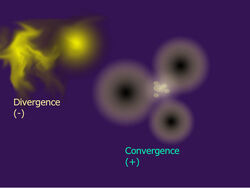
4-symmetry (or Quadrant) representation of a fractal level

	Complex	Simple
Quantized & Extreme	TeraQuasars/Quarks: Usually convergent (= quark confinement represents an upper boundary for energies being transported across sublevels within a fractal level; prevailing, not an absolute tendency) Strong Interaction (Quantum gravity/Color charge) can power objects inside a large Electric field. Balance of Electromagnetism and Strong Interaction creates complex forms. Collapse is prevented by proton repulsion.	Molecules/Protons/Electrons: Usually divergent (= electron clouds and inter-nucleon spaces represent a lower boundary for energies being transported across sublevels within a fractal level; prevailing, not an absolute tendency) Electromagnetic effects dominate causing simple periodic motion.
Continuous & Moderate	Bodies/Molecules: Electromagnetism can power objects inside a large Gravitational field. Balance of Gravity and Electromagnetism creates very complex forms. Collapse is prevented by electron repulsion.	Star Clusters/Stars/Celestial Bodies: Gravitational effects dominate causing very simple periodic motion.
Heat Capacity	Positive	Negative
When it absorbs heat, it...	Increases its temperature	Increases its period Decreases its temperature
When it releases heat, it...	Decreases its temperature	Decreases its period Increases its temperature
Greater distances	Greater force	Weaker force
Shorter distances	Weaker force Asymptotic freedom	Greater force Coulomb barrier

5 radial degrees of freedom

LEVEL	NAME	ATTRIBUTE
1	Electrons	↓ gyration radii min. ↓ more divergence
2	Bodies/Molecules	↕ the ↕ gyration radii ↕ of matter and ↕ energy fluctuate ↕ between extremes
3	Stars
4	Galaxies/Star Clusters
5	TeraQuasars/Quarks	↑ more convergence ↑ gyration radii max.
0	Void	↑ convergence traps what is below ↓ divergence blocks what is above

See also

• Big Bang
• Fractals
• Julia Set
• Mandelbrot Set
• Multiverse

References

Particles, Subatomic. (1976) The New Encyclopedia Britannica (15th ed.) Vol 13. p 1026.

(2005) Wikipedia: The Free Encylopedia

http://web.archive.org/web/20020602080635/http://www.space.com/scienceastronomy/astronomy/gravastars_020423.html

Footnotes

^  This hypothesis was formerly called Cyclical or Cyclic Multiverse Theory. K. Marinas later renamed it because the specific meaning of the word "theory" has a literal interpretation in the sciences which is different than the literal interpretation of the layman.

^  Originally, I tried defining the mass in proportion to the distance (i.e. 1E-41 when distance was 1E-41), while using the Schwarzschild radius $R_s=\frac{2GM}{c^2}$ as a guideline for how I should start investigating, but then after considering the mass of the universe in relation to a proton, I realized that it would not work that way. I dismissed that a couple times, since that would require redefining the Gravitational Constant for the lower fractal level which is described in units of $\frac{m^3}{s^2 kg}$. Years later, I still held the assumption that the speed of light would be the same for all fractal levels. Now this assumption is excised, and now objects at smaller fractal levels are predicted to move much, much faster.